原文載點:http://www2.sas.com/proceedings/sugi26/p256-26.pdf
Generalized additive model(簡稱GAM)在 1990 年由 Hastie & Tibshirani 發表出來後,就一直廣泛的被運用到許多領域中,如環境科學和醫學。GAM 的好處是沒有像其他線性模式一樣有很多的假設前提(如 normal assumption 或 variance homogeneity),而他在處理非線性模式的能力又比其他模型要來的強大。只要反應變數所服從的分配是指數族(exponential family)的一員,如 normal, binomial, Poisson, gamma 等,就可以使用 GAM。SAS 在 V8.2 版就已經納入了 PROC GAM 程序,讓使用者可以很輕鬆地用幾行指令輕易地配適出這個模型。Dong Xiang 在 SUGI 26 所發表的一篇簡單的 GAM 教學文件,讓初學者能夠在沒有足夠的背景知識下入門。
先簡單介紹一下 GAM 基本的概念。一般線性模式可如下所示:
E(Y)=b0+b1*X1+b2*X2+...+bp*Xp
但在 GAM 下,模式可改為:
E(Y)=s0+s1(X1)+s2(X2)+...+sp(Xp)
其中 si(Xi) 稱為 smooth function(或簡稱 smoother)。他們並沒有特別指定為某種方程式,而是以 non-parametric 的型態去估計。常用的估計方式稱為「backfitting algorithm」。由於 GAM 的 score equation 沒有 close form,所以必須依賴 backfitting algorithm 進行遞迴演算來估出 smoother 的參數。當然這個過程必須要交給電腦計算。
關於 smoother 的選擇有很多種,如 B-spline、thin-plate smoothing spline 或 LOESS 等等。使用者可以在 MODEL statement 直接呼叫想要的 smoother。不同的 smoother 有不同的呼叫語法,詳細情況可以上網查詢 PROC GAM 的 SAS 線上手冊。
每個 smoother 裡面會有一個參數,通常是自由度(df)。SAS 允許使用者自行決定 df ,也可以利用 GCV(generalized cross-validation)函數來挑選。
Xiang 引用了 Bell et al. 在 1989 年的一份有關駝背的醫學數據,其反應變數是一個二項變數(有(1)和無(0))。三個預測變數是 Age, StartVert 和 NumVert。資料如下所示:
data kyphosis;
input Age StartVert NumVert Kyphosis @@;
datalines;
71 5 3 0 158 14 3 0 128 5 4 1
2 1 5 0 1 15 4 0 1 16 2 0
61 17 2 0 37 16 3 0 113 16 2 0
59 12 6 1 82 14 5 1 148 16 3 0
18 2 5 0 1 12 4 0 243 8 8 0
168 18 3 0 1 16 3 0 78 15 6 0
175 13 5 0 80 16 5 0 27 9 4 0
22 16 2 0 105 5 6 1 96 12 3 1
131 3 2 0 15 2 7 1 9 13 5 0
12 2 14 1 8 6 3 0 100 14 3 0
4 16 3 0 151 16 2 0 31 16 3 0
125 11 2 0 130 13 5 0 112 16 3 0
140 11 5 0 93 16 3 0 1 9 3 0
52 6 5 1 20 9 6 0 91 12 5 1
73 1 5 1 35 13 3 0 143 3 9 0
61 1 4 0 97 16 3 0 139 10 3 1
136 15 4 0 131 13 5 0 121 3 3 1
177 14 2 0 68 10 5 0 9 17 2 0
139 6 10 1 2 17 2 0 140 15 4 0
72 15 5 0 2 13 3 0 120 8 5 1
51 9 7 0 102 13 3 0 130 1 4 1
114 8 7 1 81 1 4 0 118 16 3 0
118 16 4 0 17 10 4 0 195 17 2 0
159 13 4 0 18 11 4 0 15 16 5 0
158 15 4 0 127 12 4 0 87 16 4 0
206 10 4 0 11 15 3 0 178 15 4 0
157 13 3 1 26 13 7 0 120 13 2 0
42 6 7 1 36 13 4 0
;PROC GAM data=kyphosis;
model kyphosis = spline(NumVert,df=3)
spline(Age,df=3)
spline(StartVert,df=3)
/dist=logist;
output out=estimate p uclm lclm;
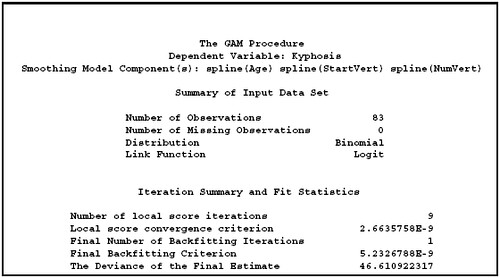
run;先來看看報表長什麼樣子。首先第一張是 Summary Statistics,裡面提供一些資料和參數估計過程的訊息,不是很重要,可以不看。
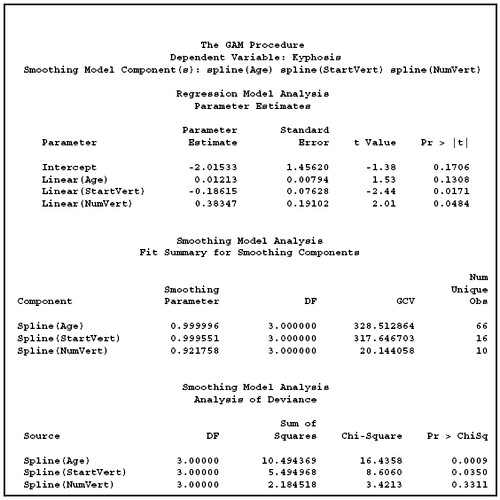
第二張才是重點。裡面包含三個報表。第一個報表表示當模式是用線性迴歸時所跑出的參數估計值。第二個報表是用 GAM 跑出的 smoother 參數估計值。第三個報表比較特別。此處利用 deviance analysis 來檢定比較 full model(包含全部 smoothing function)和 reduced model(少掉某一個 smoothing function)那個比較顯著。虛無假設則是 H0: reduce model vs H1: full model。如果後面的 p-value 小於 0.05 則表示拒絕 reduced model。反之則表示不拒絕 reduce model。以 Age 和 StartVert 來看,兩者的 p-value 分別是 0.0009 和 0.0350,皆小於 0.05。所以可以同時拒絕分別少了這兩個變數的 reduced model。而 NumVert 的 p-value 為 0.3311 > 0.05,表示不拒絕少了 NumVert 的 smoothing function 的 reduced model,亦即是說 f(NumVert) 在模式中是不顯著的。
之後可針對偏預測值(partial prediction)來做圖。偏預測值的定義是固定其餘的預測變數,來看某預測變數變動對反應變數的影響。由這些圖也可以看出預測變數的顯著性。如果預測變數的 95% 信賴區間完全涵蓋住 0 的話就表示該預測變數不顯著。
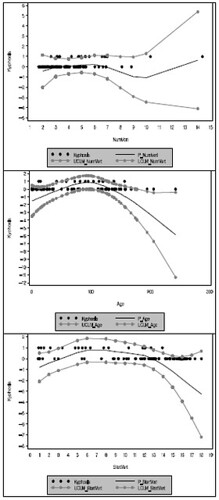
以第一張圖來看,NumVert 的 95% CI 完全包含 y=0,所以不顯著。Age(第二張圖)則是部分涵蓋,可視為顯著。比較有爭議的是 StartVert 的圖(第三張)。從圖形上來看,95% CI 應該算是完全包含了 y=0,可是末端有一小段相當逼近 y=0。原文並沒有特別說明這種情況該怎樣判斷,因此各位最好還是單純從 analysis of deviance 裡面的 p-value 來判斷,而不能完全應該偏預測值圖。此外,從 Age 和 StartVert 的偏預測值趨勢圖也可看出這兩個變數和反應變數有稍微二次項的關係。
PROC GAM 就是這麼簡單。不過,從 GAM 延伸出來的變形模式還有很多。有機會再來講 Bayesian analysis 搭配 GAM 的使用。
Contact Information
Dong Xiang, SAS Institute Inc., SAS Campus Drive,
Cary, NC 27513. Phone (919) 531-4854, FAX (919)
677-4444, Email dong.xiang@sas.com.
可是有些情況是檢定顯著,但是95%信賴區間卻都涵蓋0耶,那這是什麼情形呢?
回覆刪除請看補充內文。用偏預測圖來判定 smoothing function 的顯著性比較有爭議,所以還是以 analysis of deviance 裡面的 p-value 為主。
回覆刪除