在 mixed model 中,SAS 針對 missing data 的處理是一律先刪掉再去作分析。對使用者來說當然是一個相當方便的事情,但是就統計理論上,這種直接刪除 missing data 的動作其實潛在許多問題。比方說,如果一個資料庫裡面有十個預測變數,一個反應變數。如果其中有一個預測變數是 missing,或者只有反應變數是 missing,而其他預測變數是完整的,則整筆資料會因為少數的 missing data 而全數遭到刪除。無形間損失了許多其他存在的變數資訊,我們也應對如此的模式配適和分析結果感到懷疑。Maribeth Johnson 和 Pete Davis 在 SUGI 23 發表了一篇技術文件,專門來探討在不同的樣本大小和 missing rate 情況下,對 mixed model selection 挑選出來的 covariance structure 可能會有的影響。
Maribeth Johanson 和 Pete Davis 先是針對 Medical College of Georgia 所收集的一些重複測量的孩童血液收縮壓(systolic blood pressure,簡稱 SBP)的基本統計量和分析結果為基礎來先做資料模擬。這份原始數據顯示,孩童 SBP 的平均值是 110 mmHg,標準差是 10 mmHg。其次,根據 mixed model with TOEP covariance structure 的分析結果,四次重複測量的 correlation matrix 依序是 1, 0.7, 0.6 和 0.48。因此,模擬資料可經由下列多變量常態分配來模擬:
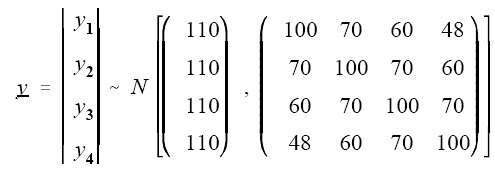
其中,x 可為隨機生成的亂數,其服從常態分配:
B 和 b 都是常數,其中 B 是 y 的 variance-covariance matrix 在 x 是獨立標準常態分配下經過 Cholesky decomposition 分解後產生的矩陣。想要用 SAS 做 Cholesky decomposition,可參考 SAS/IML 手冊。在本例中,經過分解後的 B 是:
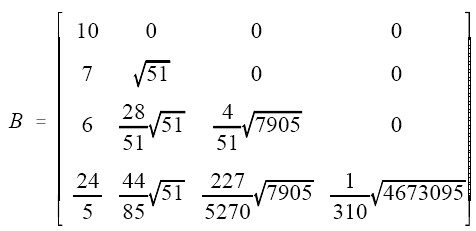
所以,y 可由下列公式模擬生成:
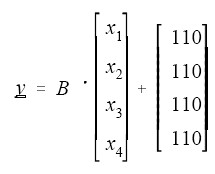
%global _PRINT_;
%let _PRINT_=OFF;
%macro simulate;
%do j=1 %to 1000;
data sbp;
do i = 1 to 150;
x1=rannor(647+i+&j*99);
x2=rannor(372+i+&j*99);
x3=rannor(425+i+&j*99);
x4=rannor(162+i+&j*99);
sbp1=10*x1+110;
sbp2=7*x1+sqrt(51)*x2+110;
sbp3=6*x1+(28/51)*sqrt(51)*x2+(4/51)*sqrt(7905)*x3+110;
sbp4=(24/5)*x1+(44/85)*sqrt(51)*x2+(227/5270)*sqrt(7905)*x3+(1/310)*sqrt(4673095)*x4+110;
output;
end;
run;
data all;
set sbp;
run;
proc transpose data=all out=allt;
by i;
var sbp1 sbp2 sbp3 sbp4;
run;
proc mixed data=allt;
class _name_;
model col1=_name_;
repeated/type=un subject=i;
make 'fitting' out=ftun&j;
run;
quit;
proc mixed data=allt;
class _name_;
model col1=_name_;
repeated/type=toep subject=i;
make 'fitting' out=fttp&j;
run;
quit;
proc mixed data=allt;
class _name_;
model col1=_name_;
repeated/type=cs subject=i;
make 'fitting' out=ftcs&j;
run;
quit;
data fit&j;
merge ftcs&j(rename=(value=val_cs))
fttp&j(rename=(value=val_toep))
ftun&j(rename=(value=val_un));
attrib simu length=$8;
simu="Sim &j ";
output;
proc datasets;
delete sbp all allt ftcs&j fttp&j ftun&j;
append base=fit new=fit&j;
run;
%end;
%mend;第二個程式是可以將上述模擬結果挑出最佳化的 mixed model。其所使用的方法當然就是傳統的 likelihood ratio test(LRT):
data pref;
set fit;
/*CS vs TOEP*/
if descr="-2 Res Log Likelihood" and probchi((val_cs-val_toep),2) gt .95 then lrtc_t='TOEP';
else if descr="-2 Res Log Likelihood" and probchi((val_cs-val_toep),2) le .95 then lrtc_t='CS ';
/*TOEP vs UN*/
if descr="-2 Res Log Likelihood" and probchi((val_toep-val_un),6) gt .95 then lrtt_u='UN ';
else if descr="-2 Res Log Likelihood" and probchi((val_toep-val_un),6) le .95 then lrtt_u='TOEP';
title1 '1000 simulations--No deletions';
title2 'Model fit information and tests of preferred models';
run;
proc print data=pref;
id descr;
where descr="-2 Res Log Likelihood";
run;
proc freq data=pref;
tables lrtc_t*lrtt_u/list;
run;- 每個觀測值的第一年數據必須保留完整。
- missing data 散佈在第二年到第四年的數據。
- 每個觀測值最多只會有一個 missing datum。
if i le 20 then sbp2=.;
if i ge 21 and i le 40 then sbp3=.;
if i ge 41 and i le 60 then sbp4=.;這會讓前 60 筆資料成為 missing data,後 90 筆資料成為 complete data。由於一開始的原始數據是隨機生成的,所以經過刪除後剩下可以拿來配適 mixed model 的 90 筆數據仍舊是維持隨機。
以下列出四個表格表示不同的 missing rate 之下和不同的 sample size 之下所配適出來的 mixed model 中最好的 covariance structure 的分佈情況:
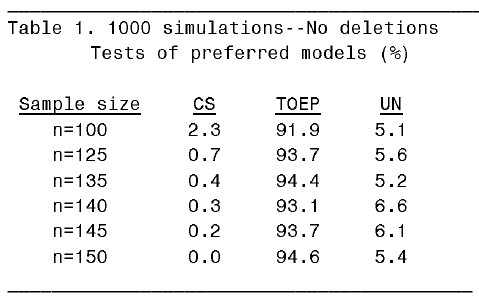

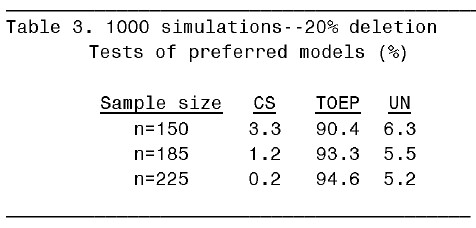
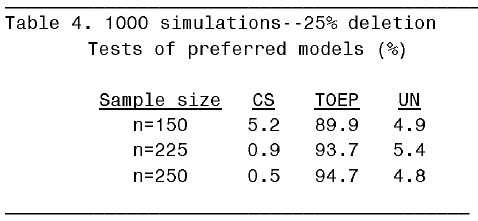
從 table 1 可知,當 n=150 時,1000 個資料集中會有 5.4% 的 UN mixed model,94.5% 的 TOEP mixed model。由於此處所設定的 Type I error 為 0.05,所以可以說在完整資料情況下,樣本數最好至少要有 150 才能有足夠的 power 讓模擬生成的數據所配適出來的 mixed model 符合原始數據所配適出來的 mixed model。在 10% missing rate 下,則樣本數要提高到 185。在 20% missing rate 下,樣本數要提高到 225。在 25% missing rate 下,樣本數得至少要 250 才行。
Author Contact
Maribeth Johnson
Office of Biostatistics, CI-104
Medical College of Georgia
Augusta, GA 30912-4900
Phone: (706) 721-3785
E-mail: maribeth@stat.mcg.edu
沒有留言:
張貼留言
要問問題的人請在文章下方的intensedebate欄位留言,請勿使用blogger預設的意見表單。今後用blogger意見表單留言的人我就不回應了。