ALPHA_CI: A SAS® Macro for Computing Confidence Intervals for Coefficient Alpha

原文載點：http://www2.sas.com/proceedings/forum2008/230-2008.pdf

在進行效度分析的時候，我們通常都會需要去求一個叫做 Cronbach's alpha的值，而這個值越大代表整個問卷設計的可信度越高。在 SAS 中可利用 PROC CORR 程序輕鬆地計算出這個數值出來，但卻沒有辦法去估計他的信賴區間。事實上，已有不少的學者發表相關文獻來估計 Cronbach's alpha 的信賴區間，而 Jeffrey D. Kromrey, Jeanine Romano 和 Susan T. Hibbard 收集了八個不同的估計方法，並將其整合在一個 macro 程式裡面。

相關的理論請參考原文以及其附錄的參考文獻。

整個 macro 的原始程式碼如下：

%macro ALPHA_CI (dsn = _last_,n_items = 100,confidence = .95);
proc iml symsize = 500;
start Bonett(N1,items,rxx,confidence,lowerCI,upperCI);
* +--------------------------------------------------------------------------------------+
Bonett 2002 method of CI computation
Inputs to subroutine are number of examinees (N1), number of items (items),
sample value of coefficient alpha (rxx), and desired level of confidence
(Confidence).
Outputs are the upper and lower limits of the confidence interval (upperCI, lowerCI)
+--------------------------------------------------------------------------------------+;
critZ = -1#probit((1-Confidence)/2);
transBon_z = log(1-abs(rxx));
if rxx <0 transbon_z =" transBon_z" var_z =" (2#items)/((items" se_bon_z =" sqrt(var_z);" lowerci =" 1" upperci =" 1" lowerf =" (1-Confidence)/2;" upperf =" Confidence" fb =" FINV(upperF,N1-1,(N1-1)#(items-1),0);" fa =" FINV(lowerF,N1-1,(N1-1)#(items-1),0);" lowerci =" 1" upperci =" 1" critz =" -1#probit((1-Confidence)/2);" transfish_z =" 0.5#log((1+abs(rxx))/(1-abs(rxx)));" transfish_z =" transfish_z" se_fish_z =" sqrt((n1-3)##-1);" upperci =" (exp(2#(transfish_z" lowerci =" (exp(2#(transfish_z" critz =" -1#probit((1-Confidence)/2);" transhawh_z =" (1-rxx)**(1/3);" var_z =" ((18#items)#(n1" se_hawh_z =" sqrt(var_z);" c_star =" ((9#n1" lowerci =" 1" upperci =" 1" critz =" -1#probit((1-Confidence)/2);" bigone =" j(N1," means =" ((bigone`)*out3pl)/N1;" score3pld =" out3pl-(bigone*means);" itemcov =" (1/(N1-1))*((SCORE3PLd`)*SCORE3PLd);" one =" j(items,1);" jtphij =" (one`)*itemcov*one;" trphisq =" trace(itemcov*itemcov);" trsqphi =" (trace(itemcov))**2;" jtphisqj =" (one`)*(itemcov*itemcov)*one;" omega =" jtphij*(trphisq+trsqphi);" omega =" omega-(2*(trace(itemcov))*jtphisqj);" omega =" (2/(jtphij**3))*omega;" s2 =" (items**2)/((items-1)**2);" s2 =" s2*omega;" se =" sqrt(s2/N1);" lowerci =" rxx-(CritZ*se);" upperci =" rxx+(CritZ*se);" lowerf =" (1-Confidence)/2;" upperf =" Confidence" fb =" FINV(upperF,n1#(items-1),n1,0);" fa =" FINV(lowerF,n1#(items-1),n1,0);" upperci =" 1" lowerci =" 1" critz =" -1#probit((1-Confidence)/2);" upperci =" 1" lowerci =" 1" parm =" J(1,7,.);" nsub =" NROW(data);" nvar =" NCOL(data);" nv2 =" nvar*(nvar+1)/2;" rsub =" 1." rs1 =" 1." vrat =" nvar" mean =" data[+,]" quant =" -1#probit((1-prob)/2);" cov =" rs1" vvar =" vecdiag(cov);" summat =" cov[+,+];" sumvars =" vvar[+];" sumcovs =" .5*(summat" wcv =" cov" wvv =" vecdiag(wcv);" sumvar2 =" wvv[+];" summat2 =" wcv[+,+];" alpha =" vrat" tmp =" 2." t1 =" summat" t2 =" summat" t3 =" 2.*sumvars" nase =" tmp*(t1" nase =" sqrt(rsub*nase);" dwrtvar =" -2." dwrtcov =" vrat" jac =" J(nvar,nvar,dwrtcov);" j=" 1" trac =" 0.;" isub="1" v =" data[isub,]" wcv =" jac" tmp =" wcv[+,+];" trac =" trac" nnase =" sqrt(rsub*rs1*trac);" i =" 1" i =" 1" item_scores =" temp_x;"> 1 then do;
Item_Scores = Item_Scores || temp_x;
End;
%end;
confidence = &confidence;
* +---------------------------------+
Computation of Cronbach Alpha
+---------------------------------+;
N_items = ncol(Item_Scores);
N_obs = nrow(Item_Scores);
mu1 = J(N_items,1,0);* ;
var = J(1,N_items,0);* ;
do k = 1 to N_items;
do i=1 to N_obs;
mu1[k,1] = mu1[k,1] + Item_Scores[i,k];* ;
end;
var[1,k]=(mu1[k,1]/N_obs)*(1 - mu1[k,1]/N_obs);
end;
sumvar=0;
do k = 1 to N_items;
sumvar = sumvar + var[1,k];* ;
end;
rowsum = J(N_obs,1,0);
do p = 1 to N_obs;
do k = 1 to N_items;
rowsum[p,1]=rowsum[p,1] + Item_Scores[p,k];
end;
end;
sumscore = 0;
sumscore2 = 0;
do p = 1 to N_obs;
sumscore = sumscore + rowsum[p,1];
sumscore2= sumscore2 + rowsum[p,1]##2;
end;
vartotal= (sumscore2-(sumscore##2/N_obs))/(N_obs);
* +------------------------------------------------------------+
Be sure we have some score variance before going any further
* +------------------------------------------------------------+;
if vartotal <=0 then do; print 'Total Score Variance =' vartotal; print 'Check the Data!'; end; if vartotal > 0 then do;
rxx = (N_items/(N_items -1))*((vartotal- sumvar)/vartotal);
if rxx < rxx =" .00001;"> .99 then rxx = .99;
* +-------------------------------------------+
Call subroutines for confidence intervals
+------------------------------------------+;
run Bonett(N_obs,N_items,rxx,Confidence,lowerBonett,upperBonett);
run Feldt(N_obs,N_items,rxx,Confidence,lowerFeldt,upperFeldt);
run Fisher(N_obs,N_items,rxx,Confidence,lowerFisher,upperFisher);
run HW(N_obs,N_items,rxx,Confidence,lowerHw,upperHW);
run ID(N_obs,N_items,rxx,Item_Scores,confidence,lowerID,upperID);
run KF1(N_obs,N_items,rxx,Confidence,lowerKF1,upperKF1);
run KF2(N_obs,N_items,rxx,Confidence,lowerKF2,upperKF2);
parm = scalpha(Item_Scores,confidence);
lowerADF = parm[1,6];
upperADF = parm[1,7];
end; * end the 'if vartotal > 0' conditional;
rxx = round(rxx,.001);
* +---------------------------------+
Printed macro output
+---------------------------------+;
file print;
put @1 'Confidence Intervals for Coefficient Alpha' /
@1 '-------------------------------------------------------' /
@1 'Level of Confidence:' @30 Confidence /
@1 'Number of Observations:' @30 N_obs /
@1 'Number of Items:' @30 N_items /
@1 'Sample Value of Alpha:' @30 rxx //
@1 'Method' @40 'Lower' @50 'Upper' /
@1 '------------------------------' @40 '-----' @50 '-----' /
@1 'Bonett' @40 lowerBonett 5.3 @50 upperBonett 5.3 /
@1 'Feldt' @40 lowerFeldt 5.3 @50 upperFeldt 5.3 /
@1 'Fisher' @40 lowerFisher 5.3 @50 upperFisher 5.3 /
@1 'Hakstain & Whalen' @40 lowerHW 5.3 @50 upperHW 5.3 /
@1 'Iacobucci & Duchachek' @40 lowerID 5.3 @50 upperID 5.3 /
@1 'Koning & Frances Exact' @40 lowerKF1 5.3 @50 upperKF1 5.3 /
@1 'Koning & Frances Asymptotic' @40 lowerKF2 5.3 @50 upperKF2 5.3 /
@1 'Asymptotic Distribution Free' @40 lowerADF 5.3 @50 upperADF 5.3 /
@1 '-------------------------------------------------------';
quit;
%mend;

以上長達數百行的原始碼，我們不需要特別瞭解內部構造，只要知道該怎樣用即可。整個 macro 包含三個參數：

• dsn：使用的 data set 名稱。如果沒有特別指定，則這個 macro 會直接使用最後一次使用過的 data set。
  
• n_items：變數數量。預設值是 1000。
  
• confidence：信賴區間大小。預設值是 0.95。
  

以下為一個小小使用範例。假設有個問卷裡面有五道題目，而每題的選項只有兩種：1 和 0。可利用下面這個 data step 完成資料輸入：

data one;
input @1 (X1 - X5)(1.);
cards;
10000
11000
11100
11110
11111
00000
10000
11000
11100
11110
11111
00000
;

欲算出 95%、99% 和 90% 的信賴區間，則只要輸入下面這三行即可：

%ALPHA_CI (dsn = one,n_items = 5);
%ALPHA_CI (dsn = one,n_items = 5,confidence=.99);
%ALPHA_CI (dsn = one,n_items = 5,confidence=.90);

以第一個 95% 信賴區間為例，報表如下：


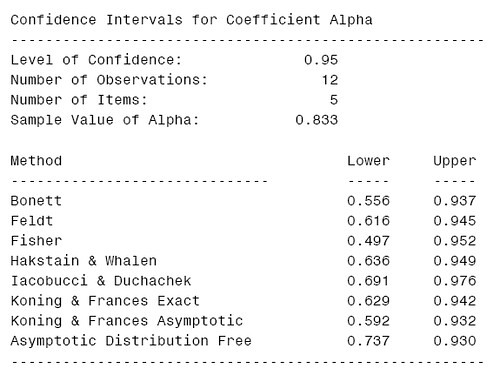
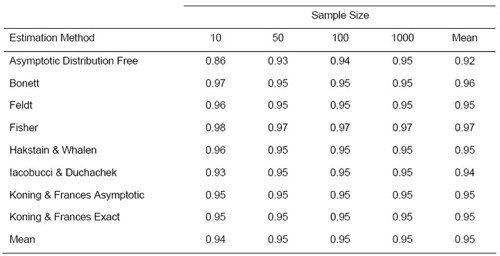
由於沒有方法去檢定哪個信賴區間是最適合的，所以作者列出下面這個表格，讓使用者根據自己的樣本大小去評斷哪種方法所算出來的信賴區間有較高的覆蓋機率（coverage probability）。


CONTACT INFORMATION
Your comments and questions are valued and encouraged. Please contact Jeff Kromrey at:
University of South Florida
4202 East Fowler Ave. EDU 162
Tampa, FL 33620
Work Phone: 813-974-5739
Fax: 813-974-4495
Email: kromrey@tempest.coedu.usf.edu