在網路上面看到有許多論文是做實證研究的人使用 factor analysis,但一方便不懂其理論,另一方面蠻幹式地去跑程式,當然跑出來的報表是有看沒有懂。每次一直重複解答同樣的問題也讓回應者感到很煩,所以在這邊就對 PROC FACTOR 做個簡單描述。我引用 Rachel J. Goldberg 所發表的技術文件,但不知道是哪一年發表的,也不曉得是在哪一期的 SUGI 發表的。不過該篇文章確實放在 SUGI 的資料庫裡面,所以就拿出來做一個簡易的範例教學。
使用 Factor Analysis 的三大目標是:
- 使用最少的因素數來解釋資料最大的變異。
- 藉著轉置因素來找尋更簡單也更容易去解釋的因素。
- 決定因素之有意義的解釋以瞭解資料本身潛在的特性,以利於更進一步的分析。
PROC FACTOR DATA=SAVE.EXAMP
METHOD=PRINCIPAL
SCREE
MINEIGEN=O
NFACTOR=16
ROTATE=VARIMAX
REORDER
OUT=SAVE.EXAMPFAC;
VAR X2--GAPLL;
RUN;簡言之,PROC FACTOR 程序裡面只有一個 VAR statement 需要拿來指定要納入整個分析的原始變數名稱(即此例的 X2 -- GAPLL)。許多內部功能,全部都只需要在 PROC FACTOR 後面的 option 來操作。以下就分別介紹每個 option 的用途:
- DATA:用來指定所使用的資料集名稱。
- METHOD:用來指定從原始變數歸納出數個主要因素所需的方法。最常使用的是主成分分析法(Principle Component Analysis),語法是 PRINCIPLE 或 PRIN 或 P。其他還有 Alpha method(語法是 ALPHA)、Harris method(語法是 HARRIS)、Unweighted least squares factor analysis(語法是 ULS)等等。不過 PRINCIPLE 仍就是最常使用的方法。
- SCREE:可以畫出特徵值(eigenvalue)的 scree plot,稍後的範例會再介紹。
- MINEIGEN:可以指定特徵值的最小值,小於這個最小值的特徵值將不會被列在報表裡面。預設值是「0」。
- NFACTOR:可以指定被歸納出來的因素的數量,預設值是等同於原始變數數量。亦即,若有四個原始變數,則會產生四個因素。如果利用這個 option 設定成只要三個因素,則最後一個因素(通常是特徵值最小的那個因素)將不會被列在報表裡面。
- ROTATE:這應該是整個程序中最重要的一個選項。轉置的功用主要是讓歸納出來的因素彼此間更有區分性和代表性。以幾何學的角度來看,轉置後的因素在空間向量裡面會更加呈現直角狀態,亦即互相獨立。但是在實務經驗裡面來看,並不是轉置過後的因素就一定會完美到這種地步,我們僅能就所能夠容忍的範圍內來採納。轉置的方法有很多種,常用的有 Varimax rotation(語法是 VARIMAX 或 V)、Orthomax rotation(語法是 ORTHOMAX)、Orthogonal equamax rotation(語法是 EQUAMAX)等等。此外,並沒有工具可以輔助來求得最佳化的轉置法,通常都是一個個去測試,看哪個結果比較容易解釋就用哪種轉置法。如果沒有指定這個選項,則因素不會被轉置。
- REORDER:這個語法只是控制報表裡面各種因素的排列方式是依照能夠解釋資料最大變異的因素排在最上面,然後依序排下來。
- OUT:可以將分析結果輸出成另一個資料集。
http://support.sas.com/onlinedoc/913/getDoc/en/statug.hlp/factor_sect5.htm
在解釋輸出報表之前,先稍微提一下特徵值(eigenvalue)的觀念,讓沒有線性代數背景的人能夠對這個怪異名詞有一點粗淺的瞭解。他最原始的數理演算過程可以參考下面個中文網頁:
http://webclass.ncu.edu.tw/~junwu/ch5_3_2.htm
在因素分析中,特徵值便是拿來製造原始變數的線性組合所需要的元素。
以下就來介紹幾個重要的輸出報表:
EIGENVALUES OF THE CORRELATION MATRIX
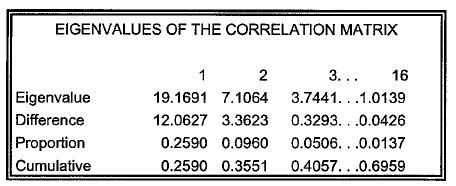
這個報表提供了所有特徵值(從大到小排列)所提供的訊息,包含:
- Eigenvalue:特徵值數據。
- Difference:和後一個特徵值的差距。
- Proportion:每個特徵值可以解釋資料變異的比例。越大的特徵值可以解釋資料的變異也越大。
- Cumulative:累積的解釋變異比例。
SCREE PLOT OF EIGENVALUE
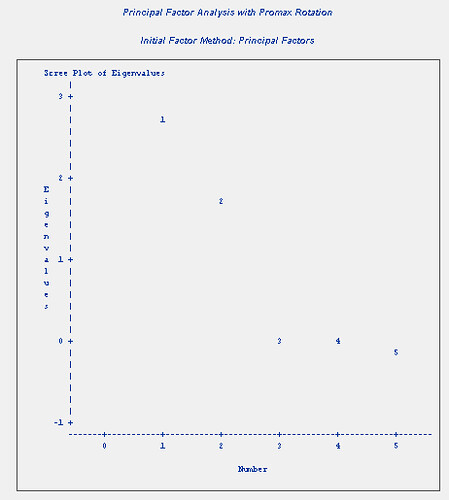
(註)原文無圖,僅以另一個 SAS 範例內的 Scree plot 來代替。
Scree plot 是把所有特徵值按大小標記在座標軸上。若將每個點連接起來,可以發現斜率越大的區段能夠解釋資料變異的能力越大。由於一開始的特徵值都比較大,所以起初的斜率都很大,到最後特徵值越來越小,整個斜率變化的幅度也會慢慢趨緩。
FACTOR PATTERN

這個表格顯示出每個因素的變異數能夠解釋原始變數變異的程度。我們稱這些數字為負荷(loading)。負荷越大代表該變數在那個因素的重要性也越大。理想上我們只希望一個變數只要在其中一個因素裡面佔有相對重要性就好,因此當一個變數在某因素出現較大的負荷,則我們就能把該變數歸納到擁有較大負荷的因素裡去。但是,在因素分析中,並沒有明確的規定多大的負荷才叫做大,通常都是以「相對比較」來看。最佳的情況是,某變數的在某因素的負荷比其他因素的負荷要來的大,並且其他因素的負荷最好是非常接近零。不過以此例的變數 X33 來看,其因素一和因素二的負荷分別是 0.42684 和 0.73425,都比因素三和因素四的負荷要來的大,可是沒有統計檢定能夠檢測出因素二的負荷使顯著大於因素一的負荷。這種情況通常都是由使用者自由心證,不過我們都會建議在遇到這種情況時,接著去做轉置(rotation)的動作。如果轉置後,X33在因素一的負荷變的更小,而在因素二的負荷卻跟著變大(當然因素三和因素四的負荷不能跟著變大),則這個轉置就有用處。轉置的方法有很多,本例是用Varimax進行轉置。轉置後的 factor pattern 會在稍後敘述。
VARIANCE EXPLAINED BY EACH FACTOR

這張表格是表示每個因素所能解釋整體資料變異的程度。數據是從大到小排列,數據越小代表所能解釋整體資料變異的程度越小,因此因素也越不重要。所有數字相加將會等於資料本身的變異數。
FINAL COMMUNALITY ESTIMATES
| Final Communality Estimates: Total = 4.669974 | ||||
| Population | School | Employment | Services | HouseValue |
| 0.98782629 | 0.88510555 | 0.97930583 | 0.88023562 | 0.93750041 |
這張表格是上面那個 factor pattern 每一行的平方和,用來表示所有因素可以解釋各個變數變異的程度。所有數據加總便是上面那個 Final Communality Estimates。
ROTATED FACTOR PATTERN
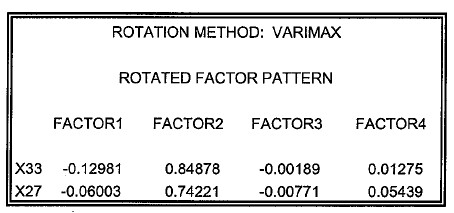
這張表格便是經過轉置過後的 factor pattern。這個 factor pattern 明顯可以看出每個變數只有在其中某一個因素擁有較高的負荷,而且其他因素的負荷都低到接近零。
不過,在這邊必須特別強調,根據個人經驗,轉置後的 factor pattern 有可能不會像本例那樣容易區分。這有可能是原始資料本來就沒有辦法進行有效的因素分析。通常解決的方法是換別的轉置法來看結果有沒有比較好。如果試過所有的轉置方法後仍沒有達到預期效果,則必須朝增加樣本數或剔除離群值等各方面來下手。
VARIANCE EXPLAINED BY EACH FACTOR

這張表是經過轉置過後每個因素可以解釋整體資料變異程度的新數據。
FINAL COMMUNALITY ESTIMATES
接下來會再看到一張 final communality estimates 的表格。這張表會和前面那張轉置前的 final communality estimates 表格一模一樣,因為轉置並不會對此處的數據產生任何影響。
以上就是幾個比較重要的因素分析表格解說。基本上大部分的分析到此,把變數歸類命名後就可以告一段落。如果打算繼續進行分析,比方說要做模式,通常把歸類好的變數加總或標準化加總,然後用新的變數去配適模式即可。
網路上有諸多關於因素分析在 SAS 下運作的文章,中英文皆有,大家可以自行 google 一下。
AUTHORS ADDRESS
The author may be contacted at
Rachel J. Goldberg
Guideline Research/Atlanta, Inc.
3675 Crestwood Parkway, N.W., Suite 520
Duluth, GA 30136
Phone: (770) 717-7844
Fax: (770) 717-7876
Email: GRCRJG@aoI.com
沒有留言:
張貼留言
要問問題的人請在文章下方的intensedebate欄位留言,請勿使用blogger預設的意見表單。今後用blogger意見表單留言的人我就不回應了。