A macro for nearest neighbor imputation

原文載點：http://www.mediafire.com/?sharekey=00ab0205b2465593dd8b33b5aa27078d

長期以來 SAS 內部只能使用 PROC MI 來執行多重插補法的資料插補動作，而當然世界上不可能只有這麼一種方法。由於多重插補法的使用時機需要配合他強大的假定，所以一旦資料不適用 PROC MI 時，SAS 使用者往往沒有別的替代方案。另外，有時缺失值的情況不嚴重，但使用 Complete Case Analysis 直接刪除有缺失值的觀測值，往往對其他沒有缺失值的變數造成一些資料上的浪費。使用 PROC MI 又需要驗證許多假定，還得在事後進行 PROC MIANALYSIS，實在相當浪費時間。如果有個簡單但又不失可靠的替代方案，將可大大增加處理缺失值的效率。Nearest neighbor imputation（以下簡稱 NNI）是個形之多年的資料插補法，但 SAS 現存的程序並不支援。這篇於 SESUG 2008 由 Lung-Chang Chien (我本人)和 Mark Weaver (我的committee member)所發表的技術文件，提供了一個簡易的 macro 來執行 NNI 的插補動作。


首先，要瞭解 Nearest neighbor imputation 的理論，可以參考這一篇文章：

Nearest。Neighbor。Imputation

我所設計的 %NNI 一共只有五個語法便可完成插補的動作。原始碼如下：

%MACRO NNI(INDATA=,                  /*INPUT DATA SET(INCLUDING LIBRARY NAME) */
MISSVAR=,                 /*INPUT SINGLE VARIABLE WITH MISSING DATA*/
RESPVAR=,                 /*RESPONSE VARIABLE*/
IDVAR=,                   /*SUBJECT VARIABLE*/
OUTDATA=                  /*OUTPUT DATA SET WITH COMPLETE DATA*/
);

DATA OBSY_MISSX;
SET &INDATA;
IF &MISSVAR=.;
KEEP &IDVAR &RESPVAR;
RUN;

PROC MEANS DATA=&INDATA N NMISS NOPRINT;              
VAR &MISSVAR;
OUTPUT OUT=OBSN N=OBSX NMISS=MISSX;
RUN;

DATA _NULL_;
SET OBSN;
CALL SYMPUT('OBSN',OBSX);
CALL SYMPUT('MISSN',MISSX);
RUN;

DATA SIMDATA_NOMISS;
SET &INDATA;
IF &MISSVAR NE .;
RUN;

PROC IML;
USE SIMDATA_NOMISS;
READ ALL VAR {&MISSVAR} INTO XMAT;
READ ALL VAR {&RESPVAR} INTO YMAT;
USE OBSY_MISSX;
READ ALL VAR {&IDVAR &RESPVAR} INTO MISSMAT;
TXMAT=T(XMAT);
TYMAT=T(YMAT);
DISTANCE=J(&MISSN,&OBSN,.);
MIND=J(&MISSN,1,.);
MISSVAR=J(&MISSN,&OBSN,.);
IMP=J(&MISSN,1,.);
DO I = 1 TO &MISSN;
DO J = 1 TO &OBSN;
DISTANCE[I,J]=ABS(MISSMAT[I,2]-TYMAT[,J]);
END;
MIND[I,]=MIN(DISTANCE[I,]);
END;
DO I = 1 TO &MISSN;
DO J = 1 TO &OBSN;
IF DISTANCE[I,J]=MIND[I,] THEN MISSVAR[I,J]=TXMAT[,J];
END;
IMP[I,]=MISSVAR[I,:];
END;
CNAME={"&IDVAR" "&RESPVAR" "&MISSVAR"};
IMPX=MISSMAT||IMP;
CREATE NNI FROM IMPX[C=CNAME];
APPEND FROM IMPX;
QUIT;

DATA &OUTDATA;
MERGE &INDATA NNI;
BY &IDVAR;
RUN;
%MEND;

語法使用方式如下：

• INDATA：原始資料的名稱，包含其所用的 library
  
• MISSVAR：含有 missing data 的變數（只能放一個）
  
• RESPVAR：沒有 missing data 的變數（也只能放一個）
  
• IDVAR：放 id number 或 case number，如果沒有的話必須要自己造一個
  
• OUTDATA：插補過後輸出的完整資料

這邊使用一個實際範例來說明如何使用 %NNI。我使用一個位於北卡 Raleigh 的空氣品質監測站的資料，使用裡面的 PM2.5 和二十四小時日均溫這兩個變數，時間點取在西元兩千年，所以總共有 366 個觀測值。其中氣溫變數是完整的，但是 PM2.5 有十七個 missing data。我用這個資料來配適下面這個模式：



程式如下：

%NNI(INDATA=CASE.RALFORNNI,
MISSVAR=PM25TMEAN,
RESPVAR=TMPD,
IDVAR=DATE,
OUTDATA=CASE.RAL_NNI); 

這張散佈圖說明了插補資料所在的位置：



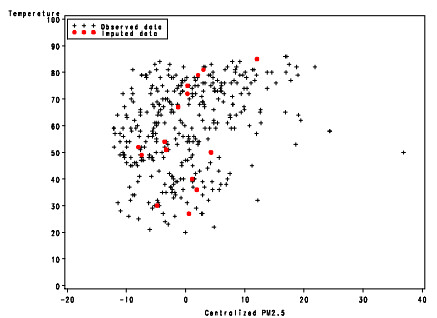
由於 Nearest neighbor imputation 是一個比較保守的插補法，所以插補值很依賴既有資料的變異程度。如果既有資料的變異程度比較小，那能夠拿來當作插補值的變化也會跟著變小。不過至少不可能插補到離群值，這一點是絕對可以保證的。

再來看看 PM2.5 在插補前後的差異：

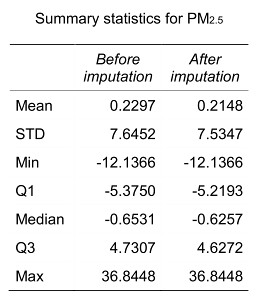
可以發現數值都很逼近。

經過 PROC GAM 程序的配適後，比較一下最重要的兩個參數估計值的結果：


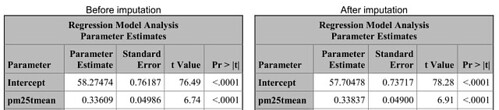
從上表可知彼此的差異不大。顯著情況也沒有改變。

再來看看平滑曲線圖：


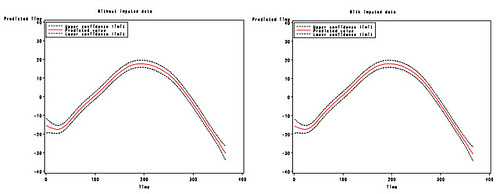
兩張圖的情況也非常近似。不過這邊要特別強調一點，那就是如果 missing data 是出現在要配適平滑曲線的變數時，Nearest neighbor imputation 的成效並不好。這一點已經經過我用另外一個模擬結果證實了，只是沒放在這篇技術文件裡面。這個實例之所以會有相似的平滑曲線是因為 missing data 只出現在線性的應變數 PM2.5 裡面，而非使用在平滑曲線的時間變數裡面。

Nearest neighbor imputation 還是有一些限制，整理如下：
1. 不太適用於插補離散變數，但如果資料夠大，能來搭配的完整變數內的數值變化也夠多的話，還是可以勉強使用。
2. 資料一定要多，太小的樣本數會大幅降低插補功效。
3. 資料裡面一定至少要有一個完整的變數，如果所有變數都有 missing data，則此方法和程式都會失效。
4. 目前這個 macro 的版本只能在 MISSVAR 和 RESPVAR 裡面各放一個變數。如果有數個變數含有 missing data，則需要重複使用這個 %NNI 來插補。如果情況是完整的變數有很多個，那到底要放哪一個變數在 RESPVAR 裡面。目前為止並沒有什麼準則來決定最好的完整變數。根據我個人的經驗，最好先用 PROC CORR 把所有變數的相關矩陣弄出來，然後挑出那個和有 missing data 變數有最高相關程度的完整變數即可。

此外，這次在 St. Pete Beach 舉辦的 SESUG 2008 會議，我也有去會場發表。整個過程可以看下面這篇文章：

St。Pete。Beach

比較令人印象深刻的是我在 Tampa International Airport 等交通車時遇到了 Wendi Wright 女士。本部落格曾經發表過兩篇她寫的 SAS 技術文件：

A Legend is Not Just a Legend
Checking for Duplicates

她今年也在 SESUG 發表了兩篇技術文件，有空我再來分享她的著作。

CONTACT INFORMATION
Your comments and questions are valued and encouraged. Contact the author at:
Lung-Chang Chien
University of North Carolina at Chapel Hill
Chapel Hill, NC 27599
E-mail: cchien@email.unc.edu